74. Search a 2D Matrix

30 Dec 74. Search a 2D Matrix

Posted at 14:38h in Coding by
0 Likes

Write an efficient algorithm that searches for a value target in an m x n integer matrix matrix. This matrix has the following properties:

 

  • Integers in each row are sorted from left to right.
  • The first integer of each row is greater than the last integer of the previous row.

Example 1:

 

 

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

 

 

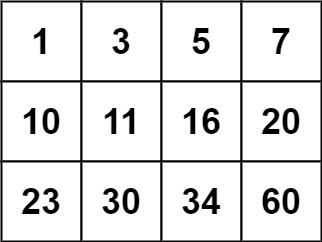
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

 

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 100
  • -104 <= matrix[i][j], target <= 104

 

class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if len(matrix) == 0:
            return False
 
        m = len(matrix)
        n = len(matrix[0])
        row = 0
        column = n-1
        while row < m and column >=0:
            if matrix[row][column] == target:
                return True
            elif matrix[row][column] > target:
                column = column -1
            elif matrix[row][column] < target:
                row = row + 1
        return False
  • Intuition, since the rows are sorted, columns are sorted as well, thus we can do 2 binary search to locate the exact position of target
  • First, handle special cases. e.g. [], [[]]
  • Second, binary search on rows, to locate row number
    • If not found, return False
  • Third, once we have row number, binary search on columns
    • If not found, return False, else return True
  • Time Complexity O(lgm + lgn) == O(lg(mn))
class Solution:
    def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
        if len(matrix) == 0:
            return False
       
        m = len(matrix)
        n = len(matrix[0])
        current_row = -1
        first_row = 0
        last_row = m -1
        while first_row <= last_row:
            middle_row = (first_row + last_row) // 2
            print(middle_row)
            if matrix[middle_row][0] <= target <= matrix[middle_row][n-1]:
                current_row = middle_row
                break
            elif matrix[middle_row][n-1] < target:
                first_row = middle_row + 1
            else:
                last_row = middle_row – 1
        print(“row————————————“)
        print(current_row)
        print(“current row————————————“)
       
        first_column = 0
        last_column= n-1

 

        while first_column <= last_column:
            middle_column=(first_column + last_column) // 2
            print(middle_column)
            print(matrix[current_row][middle_column])
            if matrix[current_row][middle_column] == target:
                return True
            elif matrix[current_row][middle_column] < target:
                first_column = middle_column + 1
            elif matrix[current_row][middle_column] > target:
                last_column = middle_column – 1
        print(“column————————-“)        
        return False
 

 

No Comments

Post A Comment